Statics - Geotechnical Engineering
Statics - Geotechnical Engineering |
|
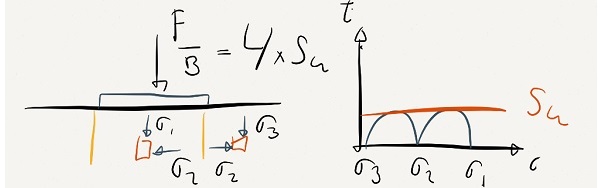
|
|
|
HOME
Kinematics Dilatancy Angle |
Static Admissible Solution |
|||
|
Updated 16.06 2013 Introduction A static admissible solution is a lower bound solution which requires equilibrium between the internal stresses and the applied loads. It is very commonly used in civil engineering to determine capacity of beams and other structural elements. In geotechnical engineering in has been used to derive bearing capacity equations. I have in the following use the approach on pile which is applied a combination of horizontal and vertical loads. Pile design
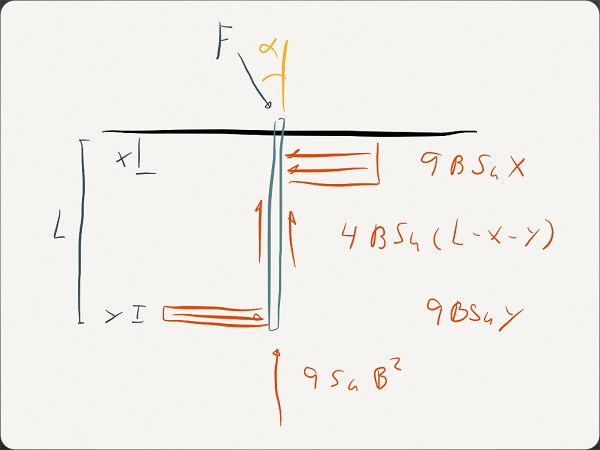
A pile is installed in a cohesive soil with the length L, width B and is applied a load F at an angle alpha. For the purpose only of illustrating a statical admissible solution I have chosen to use the horizontal capacity for the soil as rh=9B*su for the entire pie length. The vertical resistance is determined by rv=4B*Su for the side adhesion and rt=9su*B*B for the tip resistance.
A statical admissible solution requires equilibrium between the internal stresses and the applied load:
Stability EnvelopeI have determined that the maximum value for y is 0.29 and I have solved the problem in the range of y=0-0.29, L=10m, B=1m and Su=5kPa. The result is a stability envelope for the pile. The stability envelope is presented in the figure below. Discussion/disclaimer
Please be advised that the solution above have certain limitations as it assumes 9*Su*B from the surface. It is thereore only applicable for soil with density of gold and a strength of yoghurt. Such a soil is not all that common.
|
|||