|
Updated 06.10.18
review of OptumG3
INTRO
Brinch Hansen proposed in a 1968 paper to include a shape factor to account for 3D
effects for drained conditions. At the same time, he expressed the lack of 3D theory
of plasticity solutions to determine a more accurate shape factor. Since then,
all offshore design codes have included the shape factor.
Today – 50 years later – Brinch Hansen would be delighted! Now there is a plasticity
3D software available. In the following, I will test the FELA software OptumG3
(version 2018.07.30 (1.3.0.14261)) with an offshore foundation initial vertical
loaded followed by a horizontal load causing torsion and overturning.

OptumG3 is the first commercial available 3D finite element limit analysis FELA
software commercial available. It must be mentioned that Oxford University Professorial
Research Fellow Chris Martins developed OxLim – both 2d and 3D FELA before the release
of OptumG3. OptumG3 has both FELA and some soil models in FEA. It is currently relatively
new and the user manuals are not yet available, but there are a high number of great
demo videos on youtube. User manuals should be available in 2019 along with more
advanced FEA soil models. OptumG3 uses adaptive mesh, which means that it makes an
initial mesh and improves the mesh over a few iterations to determine a more accurate
solution. Compared to Plaxis, where the user must define the mesh – and the solution
depends on how well the user defines the mesh. Hereby, OptumG3 reduces the possibility
of user errors.
CASE
Foundation is 6 x 20 m and 3.5 m high. The software is easy to use, like a very simple
drawing program. It is very critical to understand how the geometry select function works.
There are good youtube videos to help to get started. The first case I tested was bearing
capacity for vertical load. To compare it best with bearing capacity formulations,
I chose to use phi=30 and submerged unit weight of 11kN/m3 and a c’ = 0.01. I have used
the mixed element and the MOSEK solver (also used by OxLim). In 4 min I get 58,691kN,
compared to Brinch Hansen bearing capacity of 59.677kN (shape factor=1), 52.515kN
(shape factor=0.88). I compare to Plaxis 3D and get 59,700kN after approx. 2 hours of FEA.
I believe that Brinch Hansen would have been very pleased to be able to be reduce
uncertainty in the design and that he would probably have modified the shape factor.
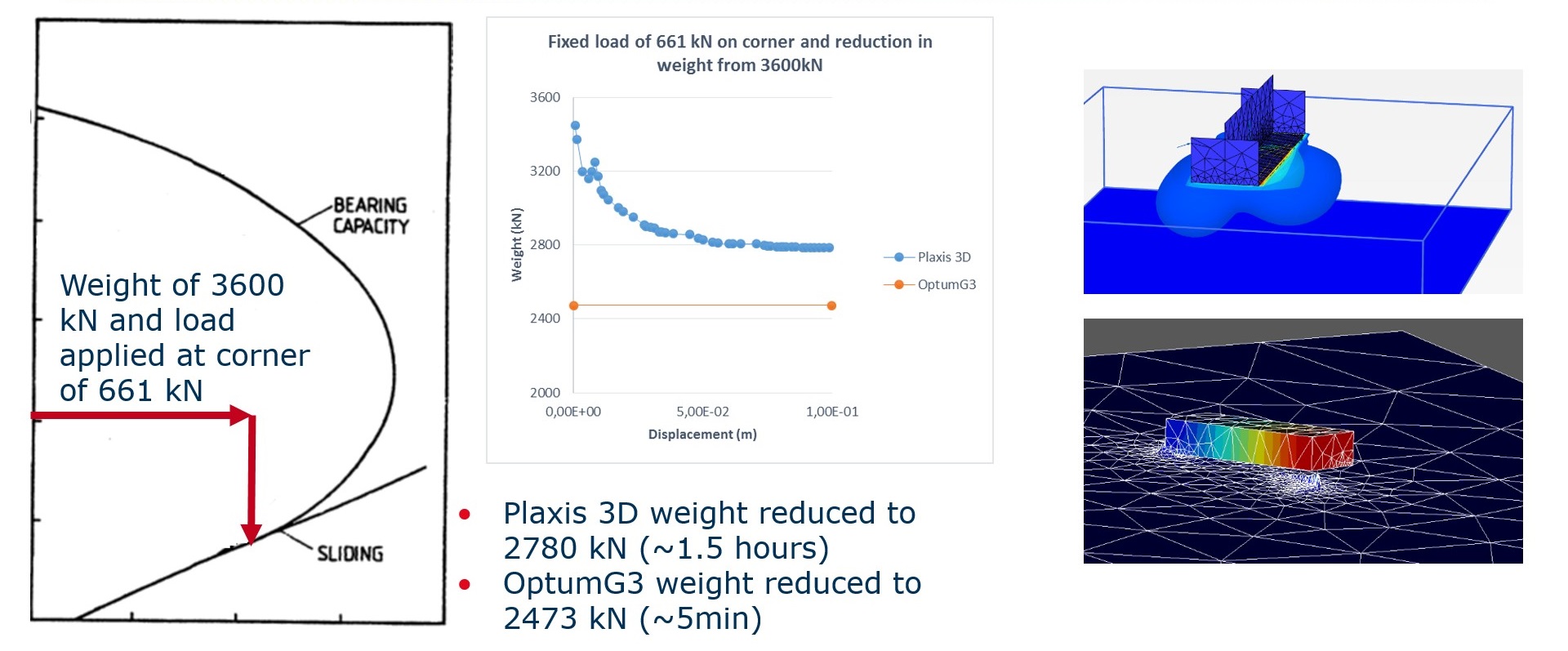
The second case I have tested is a load is applied to upper corner at 20deg to horizontal.
The load is 661kN. The soil strength is c’=3.2kPa and a friction angle of 29.7deg with a
submerged unit weight of 11kN/m3. I start of with a submerged weight of 2400kN on the
foundation and reduce the weight until failure. I get 2473 I OptumG3 and 2780kN in
PLAXIS 3D. I am a bit surprised over this relative large difference. The OptumG3
analysis is approx. 5 min while PLAXIS need to generate the full load – displacement
curve and the time is 1.5 hours. I am using an older version of PLAXIS which may
cause this difference. The analysis is illustrated below.
COMMENTS
The OptumG3 software is a great tool to determine the ultimate capacity of a foundation.
It is based on FELA which makes it very fast compared to FEA analysis. The software is
very user friendly. Manuals are yet not available, but they will be here soon. Most
geotechnical engineers have gotten used to the FEA – load displacement approach which is
in fact not the origin of the ultimate capacity analysis. This software does to some
extend bring us back to basic – back to what Brinch Hansen did not have available when
he proposed his bearing capacity formulation above. It has been 50 years since he
expressed the lack of a 3D plasticity solution to the bearing capacity and I believe
this software is finally here.
FURTHER READING
If you find the concept of FELA interesting but want to know more before you want to
implement, then I propose to read Helen Dunnes excellent and very well written phd thesis
which is found here
The thesis explains the FELA theory in further detail and presents results of several very relevant offshore aplications.
|






