Foundation Design APP - Determines undrained bearing capacity

Foundation Design APP - Technical Background

Updated 05.07 2013 - under construction

General

We have created an App for your Iphone which is based on a kinematic admissible solution. The purpose of the App is to provide a fast estimate on the foundation size when you are away for your computer. The estimate must be accompanied by detailed geotechnical design.

This page outlines the features of the App and the teoretical background. The App consists of two pages, one with the calulation and one with info. The two pages are illustrated below.

App Input

The input must be design loads and strength, i.e. you must apply safety factors in accordance to design codes such as DNV, ISO or API. Note that the foundation is defined as 1 m long which must be reflected in the applied loads The four variables are:
1. Width of foundation given in meter,
2. Su is the undrained shear strength of the soil given as kilopacal,
3. Horizontal load given in kilonewtons per meter foundation,
4. Vertical load given in kilonewtons per meter foundation.

Stability Envelope - Graph

The stability envelope is plotted as a blue line. The approach is similar to DNV Foundation Design 30.4. If the load shown as the green snowflake is located inside the stability envelope, then the design is safe. If the snowflake is located outside the stability envelope, then the solution is not safe and the width needs to be increased or the load decreased.

Kinematic admissible solution

In the good old days of geotechnical engineering, a kinematic admissible solution was frequently used to determine the capacity of a foundation. Nowadays, finite element software is used so frequently that many geotechnical engineers have forgotten how to use a kinematic admissible solution. A kinematic admissible solution is a guess on how I foundation will fail. The kinematic Admissible solution is per definition an upper bound solution. That means that if your guess the correct failure mechanism, your result will be correct. If your guess is wrong, your guess will be higher than the correct solution.

The guess in the App

The guess on a failure mechanism as seen below for a foundation with the width B and an inclined load F. I have guessed that the failure mechanism consists of three triangles. Two of the triangulars have 60° in each corner and the third is a function of theta. The soil consistent of clay with undrained shear strength su. I have not been able to find this problem solved by anyone else; However, I'm sure someone must have.

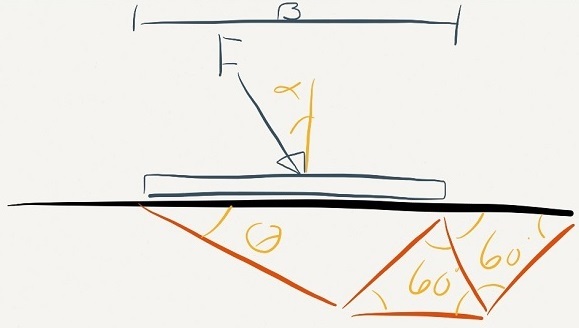
Solution found with vitual work

The foundation capacity is found with use of virtual work. I won't spend any time discussing what I did other than to mention that even virtual work might be hard work. The solution:

F = B*su*(sin60/sint + sint/tant + sint/tan60 + sint/cos60 * (1/tant + 1/tan60) + sint/sin60) / (sin(120-t)*(cosa + sina/sint))

Minimizing energy

The capacity of the foundation F is minimum of the equation above for any alpha. If you were to assume that B equals 1 and su is equal to 1, then you may plot F as a function of alpha. I have done so below.

Stability Envelope

The graph above illustrates the stability envelope for the foundation. I have now illustrated how a kinematic admissible solution may be used to determine the stability of the foundation. Compared to the DNV 30.4 solution my kinemtic solution is relative good.